离子液体的自由和束缚态下的离子及其电导率与欠屏蔽悖论
研究亮点:
1. 证实了离子液体中离子的两种状态:自由与束缚,并定量描述了两种状态的比例。
2. 构建了离子自由-束缚态的“离子半导体”模型与动力学模型。
3. 以此模型实现了对离子液体电导率的准确预测。
研究背景:
离子液体是仅由阴阳离子组成的液体,在室温下仍呈液态。除了热稳定性好、挥发性低、不可燃不爆炸等优点,相比常用的水或有机溶液电解质,离子液体具有更高的工作电压(4~6 V)。近些年来,用作储能装置(如电池和超级电容器)、电润湿技术、场效应晶体管、电化学传感器等所需的电解质,离子液体正受到越来越多研究者的关注和重视。
从化学角度来看,合成离子液体的阴-阳离子组合有无限多的可能。从物理角度来看,离子液体是一种独特的液体:具有强库仑相互作用的致密的室温等离子体。为了表现其电解质特性,离子液体中的离子必须能够移动电荷。但是它们如何在如此致密的环境中移动电荷的呢?在运动过程中离子展现什么样的动态特性呢?
成果简介:
有鉴于此,华中科技大学冯光教授、俄罗斯库尔斯克州立大学Brilliantov教授、以色列特拉维夫大学Urbakh教授和英国帝国理工学院Kornyshev教授(共同通讯作者)结合分子动力学模拟与速度自相关函数的理论分析,通过对几种典型室温离子液体中离子动态特性的系统研究,定量分析了离子液体中自由和束缚态的离子比例,构建了离子液体的自由-束缚态模型,并以此模型实现了对离子液体电导率的准确预测。
要点1. 自由-束缚态动态评估标准:离子轨迹密度法
作者首先根据离子轨迹数据证实离子确实存在于两种状态(图1):自由态和束缚态。然后根据动态评估标准,提出“离子轨迹密度法”,定量区分出两种运动状态。再通过分析所有单个阳离子和阴离子的运动轨迹,估算了离子在自由运动态及束缚态的平均滞留时间。由此,估算出在300-600 K的温度区间内,自由离子的平均含量为~15-25%,且随着温度升高而增加。作者进一步构建了基于自由-束缚态的“离子半导体”模型,发现其价带和导带的带隙为~26 meV——离子可在自由和束缚两种状态之间很容易地转换。

图1. 离子液体[Bmim][TFSI]的两种不同运动状态。阳离子(a)与阴离子(b)的运动轨迹示意图;阳离子(c)与阴离子(d)的轨迹密度云图;自由离子含量(e)与“离子半导体”模型(f)。
要点2. 离子自由-束缚态模型的动力学分析
然而,离子在自由与束缚态的运动及转换的物理机制是什么呢?作者首先分析了离子在两种不同状态下存活概率函数(图2)。如果转换过程是泊松过程,那么它们的存活概率函数是单指数型。而从图2(a)中可以看出,对于自由与束缚态,在不同温度下,离子的存活概率函数均为双指数型,这表明离子在不同状态间的交换过程为有记忆效应的非泊松过程。同时,作者定量地分析了离子在自由与束缚态的平均滞留时间,发现其随着温度的升高而降低,且阳离子与阴离子的平均滞留时间一样。
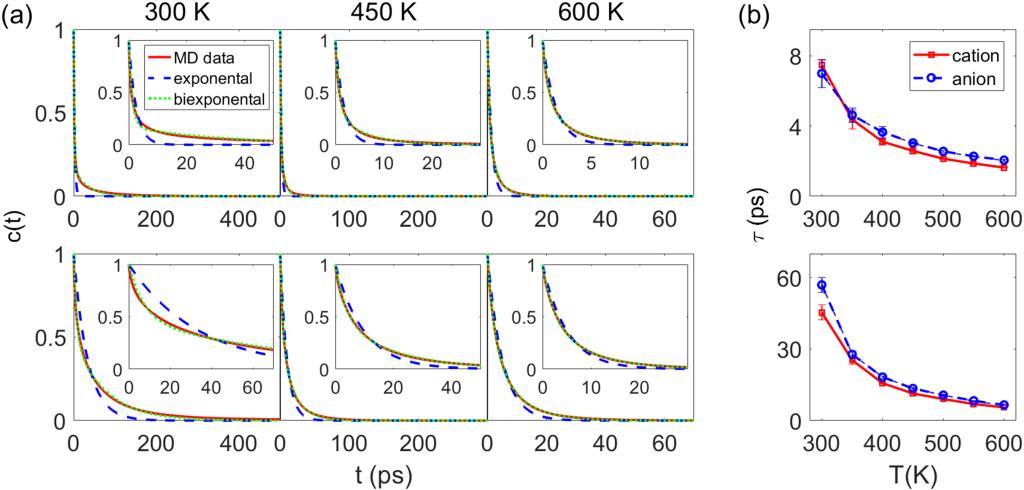
图2. 离子自由-束缚态的动力学模型。(a)自由态阳离子(上)与束缚态阳离子(下)的存活概率函数;(b)自由态离子(上)与束缚态(下)离子平均滞留时间。
为了定量的描述离子的运动特性,作者研究了离子在不同状态的速度自相关函数及其与温度的关系(图3)。进一步,作者利用非泊松过程的时间相关函数,探究离子自由与束缚状态下的速度自相关函数与系统中离子整体的速度自相关函数的关系,发现系统中离子整体的速度自相关函数可以简化为自由与束缚态的线性叠加。
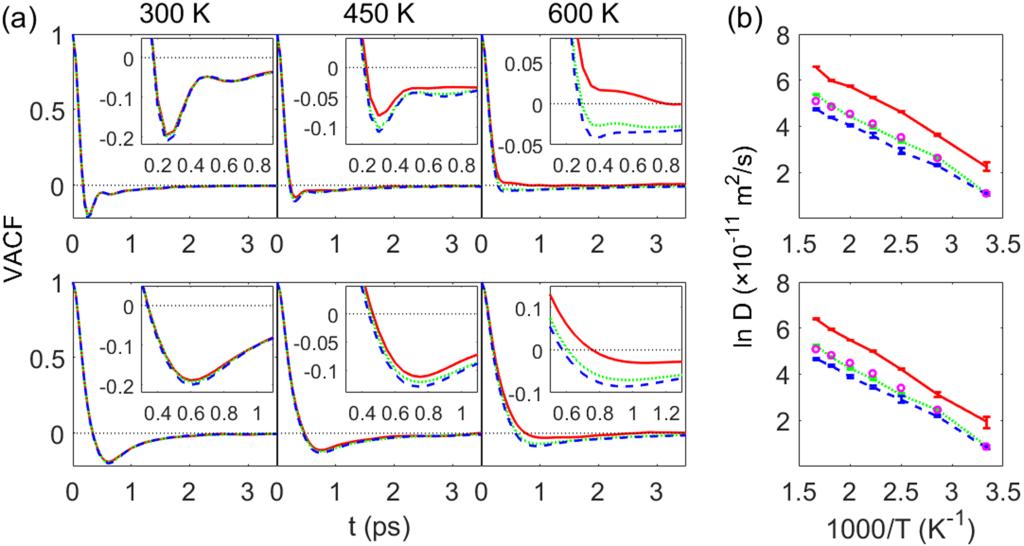
图3. 离子运动特性与温度关系。(a)阳离子(上)与阴离子(下)的速度自相关函数;(b)阳离子(上)与阴离子(下)的扩散系数。红色实线、绿色虚线和蓝色短划线分别代表自由离子、所有离子和束缚离子;(b)中品红圆圈为扩散系数实验值(J. Phys. Chem. B 109, 6103 (2005))。
要点3:离子液体电导率
离子液体中离子具有很强的库伦相互作用,原始的Nernst-Einstein方程一般会高估离子液体的电导率。如图4所示,考虑离子间的耦合,通过积分电流自相关函数得到的电导率可以与实验值吻合。进一步,作者通过自由离子的定量分析,修正了Nernst-Einstein方程,以此预测的电导率可以与通过积分电流自相关函数得到的电导率一致,且能很好的再现实验数据。
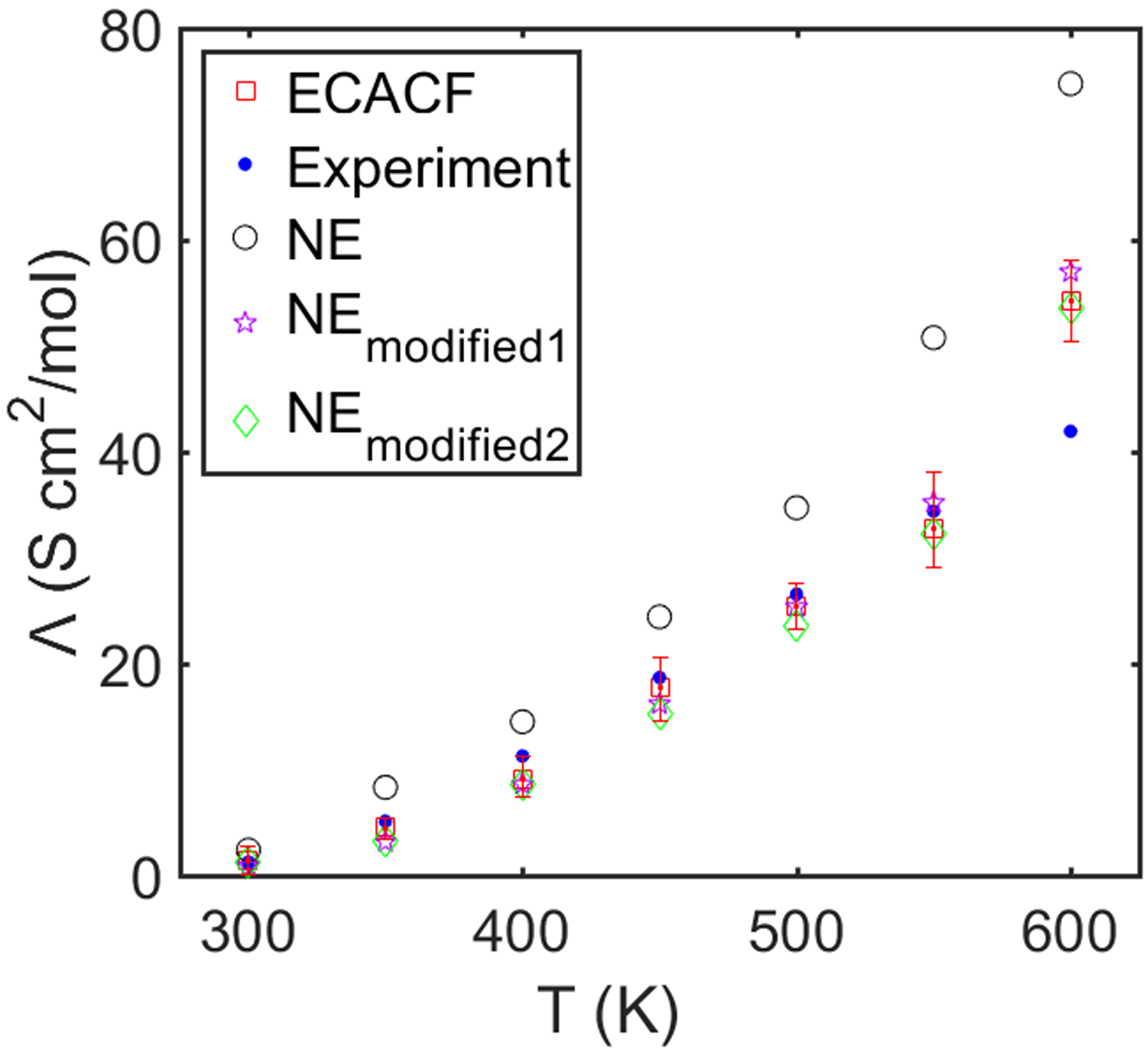
图4. 离子液体电导率与温度关系。(实验数据来源:J. Chem. Eng. Data 60, 1495 (2015))
要点4:普适性研究
最后,作者分别从空间尺度(不同的离子对数)和时间尺度(不同的模拟时长)做了同样的分子动力学模拟研究,发现这些因素对模拟结果没有影响。此外,作者也通过分子动力学模拟系统地分析了其他离子液体([Emim][TFSI]和[Bmim][PF6]),发现之前的结论在模拟上仍然成立。这说明本文的结论具有一定的普适性。
小结
启发于美国Israelachvili院士的工作(PNAS 2013, 110, 9674)——“欠屏蔽悖论”,作者结合分子动力学模拟与速度自相关函数的理论分析,系统地研究了几种典型室温离子液体中离子动态特性。从离子的运动轨迹出发,证实了离子确实存在两种状态:自由与束缚态,并定量分析了不同状态的离子比例,构建了离子液体自由-束缚态的“离子半导体”模型。进一步,通过构建自由-束缚态的动力学模型,揭示了两种状态的离子运动特性及物理机制。同时,根据自由离子的定量分析结果,修正了Nernst-Einstein方程,以此预测出的电导率很好地再现了实验数据。
该工作得到了国家自然科学基金项目和深圳市科技计划基础研究项目的资助。
论文链接:https://link.aps.org/doi/10.1103/PhysRevX.9.021024
研之成理报道
https://mp.weixin.qq.com/s/DRIfjAGoBEsvUJ5uQvboOQ